샤미르의 비밀 공유(SSS, Shamir's Secret Sharing)

개발관련/삽질

샤미르의 비밀 공유(SSS, Shamir's Secret Sharing) - 이론

동팡 2020. 5. 7. 14:41

해당 글은 이론/실무편으로 나누어져있다.

이론은 SSS의 이론에 대한 설명이며, 구현체 분석은 GitHub의 SSS 구현체 중 스타 지수가 높은 프로젝트의 소스코드를 분석한다.

개요

비밀 공유(secret sharing)는 비밀키의 소유자가 1명이 아닌 다수의 인증된(authorized) 참가자(participant) 들이 되고, 이 때 임의의 참가자는 비밀키의 일부 조각을 소유하게 되는 것이다. 예를 들어, 임의의 그룹 내에 n명의 인증된 참가자가 존재할 경우 비밀키를 n개의 조각으로 분리하여 참가자들에게 각각 비밀 조각 1개씩 나눈다. 이 중 적어 도 n명 이상의 인증된 참가자들 모이면 이들의 비밀 조각들을 이용해 본래의 비밀키(또는 비밀데이터)를 알게 된다.

즉, 비밀키의 조각을 나눠 갖은 3명이 존재한다. 해당 비밀키를 복구하기 위해서는 무조건 3명이 존재해야 한다.

이론 - 개념

선 1줄 요약: 선을 정의하는데 필요한 점의 수

SSS의 이해 – 1

일차 함수 그래프를 통한 비밀번호 공유

참석자: A, B, C

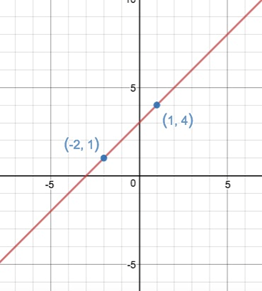
A는 위의 그림과 같은 공식(y = x + 3, 일차 함수 그래프)으로 비밀번호를 생성하였다.
A는 비밀번호를 복구를 위해, BC에게 (-2, 1)과 (1, 4)를 각각 공유하였다.
1. B 또는 C는 혼자서 비밀번호를 구성(완성)하지 못한다.
2. 점에서 선을 정의하기 위해서는 수많은(거의 무한의) 경우의 수가 존재하기 떄문이다.
만약 B, C가 합의를 한다면 비밀번호를 생성할 수 있다.
위와 같이 B, C의 부정행위를 방지할 수 없다.

SSS의 이해 – 2

이차 함수 그래프를 통한 비밀번호 공유

참석자: A, B, C, D

A는 위의 그림과 같은 공식(y = x^2 -3x + 3, 이차 함수 그래프)으로 비밀번호를 생성하였다.
1. A의 베프는 D이다. 이 친구는 절대 배신을 하지 않는다.
A는 비밀번호를 복구를 위해, BCD에게 (1.5, 0.75), (0, 3), (3,3)의 값을 각각 공유하였다. 그리고, 자기 자신은 (2, 1)을 갖고 있는다.
1. B, C와 공모를 하였지만 비밀번호를 추측하지 못한다.
2. 해당 공식은 3개의 점이 필요하기 때문이다.
만약 A는 비밀번호를 깜박하여, 비밀번호의 재생성이 필요하다.
BCD를 소집하여, 비밀번호를 생성한다.
만약 C가 해당 값을 잃어버리거나 또는 해당 값이 compromised가 되면 ABD는 소집하여, 해당 값을 생성한다.
해당 값으로 다시 그래프를 생성한 후, ABCD는 새로운 인자를 나눠 갖는다.

해당 공식은 3개의 점만 필요하지만, 보안을 위해 공식을 재구성할 수 있다. 예를 들어, 5, 10, 15개 그 이상의 점을 필요로 하는 것이다. 위의 예는 2차 함수 그래프이며, 구성을 위해 최소 3개의 점이 필요했다. 해당 사항을 4,5,6차 함수 그래프를 사용한다. 그러면, n차 함수 그래프는 n+1의 점으로 그래프를 형성할 수 있다. 아래와 같이 방정식으로 표현할 수 있다.

이것을 (t, n) threshold secret sharing이라 칭한다. n개의 비밀 조각들을 제공하고 비밀을 재구성하려면 최소 t조각의 임계 값이 필요하다. 위의 사항은(3, 4)이다. 이게 바로 SSS의 기본 이론이다. t-1차 다항식이 후보로 존재하여 원래의 다항식을 추측할 수 없다. 즉, t개보다 적은 비밀 조각이 모이더라도 원래의 비밀 값은 알 수 없다.

이론 - 기본

Preparation

우리의 Secret은 1234이다(S = 1234).

해당 Secret을 6조각으로 분리한다. 6조각(n = 6) 중 3조각(k = 3)이 모이면 Secret을 생성할 수 있다. k – 1 값은 166, 94이다.

은 Secret이다.

여기서 마지막 k 값 즉, 마지막 공유 조각을 만드는 식은 아래와 같다.

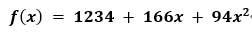
Reconstruction

Secret은 3개의 조각만 있으면 만들 수 있다. 2, 4, 5를 통해 Secret을 생성하면 다음의 식과 같다.

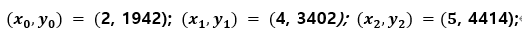
해당 식은 라그랑주 다항식[1]을 통해 아래와 같이 연산할 수 있다

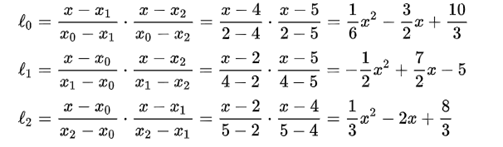
해당 식을 시그마 공식으로 유도 후 계산하면 아래와 같다.

Secert S 값을 구할 수 있다.

해당 값은 아래와 같은 수식으로 표현(간소화)할 수 있다.

[표현 - 1(방정식 나열)]

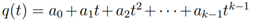
[표현 - 2(방데르몽드 행렬)]

[표현 - 3(시그마 합공식)]

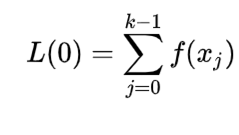
이론 - 응용

위의 식은 SSS의 기본 식이다. 위의 다항식은 정수 산술을 사용하기 때문에 안전하지가 않다. 공격자는 그래프의 포인트를 얻을 때마다, 포인트 경우의 수가 줄어든다. 예를 들어, 5차 함수 그래프를 그릴 때, SSS의 k는 6이 된다. 즉 임계치는 6이 되며 6조각이 모이면 S를 유도할 수 있다. 그런데 공격자가 k-1까지의 값을 갖고 있으며, 해당 값으로 그래프를 표현해본다. 그러면 얼추 다음의 지점의 경우의 수가 많이 감소한다. 해당사항을 시각적으로 확인할 수 있다(상상해보라).

해당 문제는 다음과 같이 해결할 수 있다.

소수의 모듈러 연산을 통해 그래프를 꼬아 버린다.

모듈러 연산에 사용하는 소수 값의 조건은 아래와 같다. 아래의 조건을 설명하면 다음과 같다. P 즉, prime(소수) p는 n(공유 조각들)보다 크고, S(비밀값)보다 크다. 는 prime의 집합이다. p는 그냥 소수라는 의미이다.

예는 아래와 같다.

k or t = 3

n = 6

k-1 = 166, 94

S = 1234

P = 1613

공유 비밀의 값이 1234일 때 우리는 아래와 같은 SSS 공식을 사용하여, 비밀 조각을 생성할 수 있다.

[공유 비밀 생성]

[비밀 재구성 – 1(basic)]

설명

1. 유리수의 modulo 연산의 경우, 정수가 될 때까지 + 또는 – 연산을 통해 정수로 변경한다. 그 후, modulo 연산을 진행한다.

2. 음수의 modulo 연산의 경우, 일반 양수 mod 연산 후, 음수로 변경한 후, m을 더한다(예: -22 mod 5, 22 mod 5는 2이다. -2 + 5 = 3. 즉, -22 mod 5는 3이다.

[비밀 재구성 – 2(optimized)]

공유를 재구성할 때 아래의 식을 적용한다(j, m의 index가 0부터 시작할 때).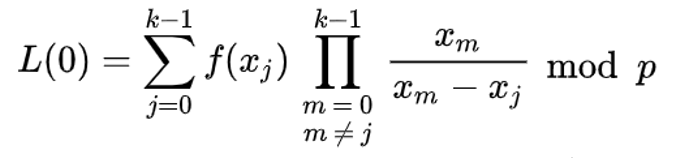

식의 풀이는 다음과 같다(i, j의 index가 1부터 시작할 때)

위의 식이 최적화 식인 이유는 아래와 같이 필요한 지수에 대해서만 연산을 하기 때문이다(우리가 알고 싶은 것은 0차항 즉, Secret 값이다.). 즉, 1234 + 166x + 94x^2의 값 중에 필요없는 166과 94는 연산에서 제외하고, 비밀 값 1234만 연산한다.

[대입]

장점

Shamir’s secret sharing의 특징은 모든 구성원이 나눠갖는 비밀이 서로 유일(unique)하며 평등하다는 것이다. 또한 threshold 이상의 조각만 있으면 secret를 복구할 수 있기 때문에 일부 비밀 조각이 유실되더라도 안전하고, 소수의 배신자가 있더라도 secret을 복구할 수 없다.

단점

이런 특징들은 한계점이 되기도 한다. 모든 shared secret이 동등하기 때문에 비밀을 나눌 때 보안 등급에 따라 나누기가 힘들고, 비밀 조각을 제공할 때 일부러 틀린 비밀 값을 주는 것을 방지할 수 없으며 비밀을 복구할 때도 누군가 오염된 값을 줘서 비밀이 제대로 복구되었는지 알 수 없다.

그러나, 이와 같은 단점들은 타계층(예: 어플리케이션 계층)에서 보완하면 되는 부분이라 생각한다. 즉, 단점이라기보다는 필요 보완사항이 되겠다.

보안

SSS의 보안 내성은 정보 이론적 보안(Information-theoretic security)이다[1]. 정보 이론으로부터 순수하게 파생된 암호시스템이다. 공격자가 암호를 깨기 위한 충분한 정보가 있지 않은 이상, 공격자의 전사 공격(brute force attack)으로부터 안전하다. 즉, 공격자가 아무리 (t, n) 구성 요소 중 t-1의 값을 갖고 있어도 안전하다. 쉽게 생각해서 “점1개를 이용하여, 선을 예측하라”이다. 가능한가?