Python TensorFlow를 이용한 몸무게 예측 프로그램
목차
프로젝트명
개요
데이터셋의 구성 현황
학습 전략
전처리
데이터 셋의 시각화
가설 정의
학습 알고리즘
비용 함수
옵티마이져
학습
데이터 검증
요약
한계
GitHub
프로젝트 명
병무청 신체 측정 정보를 통한 체중 예측
개요
공공데이터 포털에서 병무청 신체 계측 정보를 제공 받는다. 해당 데이터는 군대를 가기 위한 20대 남성의 신체정보를 계측한 데이터셋이다. 해당 데이터 셋을 학습 시킨 후 다음과 같이 체중을 예측한다. 신장, 허리 둘레, 가슴 둘레, 머리 둘레, 발 길이 값을 통해 체중을 예측한다. 데이터 셋의 구성은 아래와 같다. 학습방법은 대표적인 기본 방법인 선형 학습법을 사용한다.
데이터셋의 구성 현황
|
항목 |
설명 |
비고 |
|
성별 |
남 |
|
|
연령 |
20대(대부분 20대 초반) |
|
|
데이터 개수 |
135,670 |
|
|
데이터 구성 |
순번, 날짜, 가슴 둘레, 소매 길이, 신장, 허리 둘레, 샅 높이, 머리 둘레, 발 길이, 몸무게 |
|
|
데이터 단위 |
cm |
|
|
데이터 계측 기간 |
2013 ~ 2016 |
|
항목 |
설명 |
비고 |
|
순번 |
순번 값 |
|
|
측정 일자 |
yyyyMMDD 또는 yyyy |
|
|
가슴 둘레 |
가슴둘레(단위: cm) |
X1 값 |
|
소매 길이 |
소매 길이(단위: cm) |
|
|
신장 |
신장(단위: cm) |
x2 값 |
|
허리 둘레 |
허리둘레(단위: cm) |
X3 값 |
|
샅 높이 |
실제 다리 길이(단위: cm) |
|
|
머리 둘레 |
머리둘레(단위: cm) |
x4 값 |
|
발 길이 |
발길이(단위: cm) |
x5 값 |
|
체중 |
체중(단위: cm) |
y 값 |
학습 전략
해당 데이터셋을 통해 지도학습을 하기위해서는 아래와 같은 절차가 존재한다.
1.가설 정의
2.학습 알고리즘 선정
3.학습을 위한 코스트 함수 정의
4.코스트를 낮추기 위한 옵티마이저 정의
5.학습률 및 횟수 정의
6.학습 및 데이터 검증
“보통, 키가 크면 몸무게가 높다.” 또는 “보통, 허리 둘레가 크면 몸무게가 높다.” 와 같이 가설을 잡는다. 해당 가설을 입증하기 위해, 데이터 학습과 검증을 진행한다. 데이터 학습을 진행하기 위해서는 가설에 상응하는 학습 알고리즘 선정, 코스트 함수 정의, 옵티마이저 정의가 필요하다. 해당 가설은 선형 회귀(Linear Regression)알고리즘을 통해 학습을 진행하며, 해당 학습 Cost를 최소화 하기 위해, 경사하강법(Gradient Descent) 알고리즘을 적용하여, Cost의 저점을 찾는다. 경사하강법의 학습 폭은 학습률(Learning Rate)을 통해 조절할 수 있다.
전처리
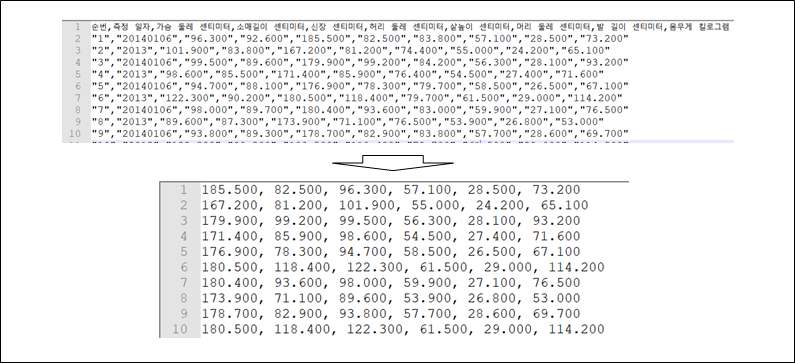
해당 데이터셋은 CSV 형식으로 제공받을 수 있기 때문에 전처리 작업이 매우 수월하다.
데이터셋에서 학습에 사용할 데이터는 “가슴 둘레, 신장, 허리 둘레, 머리 둘레, 발 길이, 체중“ 이다. 여기서 체중을 제외한 5개의 값은 입력 값이며, 체중은 출력 값이다.
데이터 셋의 시각화
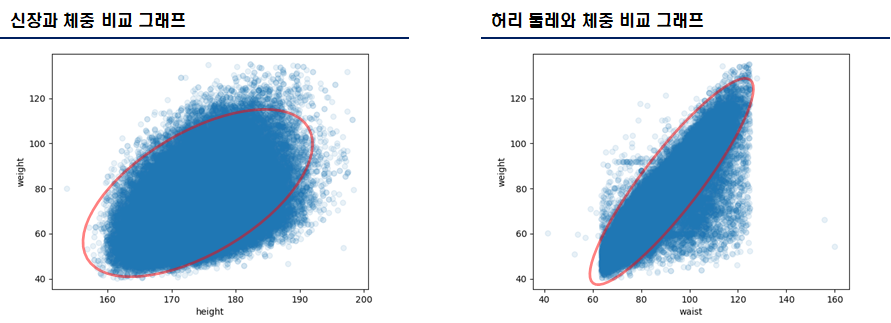
- 해당 데이터셋에서의 신장, 허리 둘레, 체중을 시각화하였을 경우, 약한 선형 구조를 그릴 수 있다. 즉, 상관관계가 존재한다.
- 허리 둘레와 체중 비교 그래프를 통해 허리 둘레가 크면, 체중도 크다는 사항에 대해 이해할 수 있다.
- 신장과 체중 비교 그래프는 규칙이 존재하지 않는다.
- 허리 둘레와 체중 비교 그래프는 약한 선형 구조이다. 강한 선형구조를 도출하기 위해 “신장”, “가슴 둘레” 등과 같은 값을 통해 강한 선형 구조를 그릴 수 있다. 즉, “허리 둘레(x1) + 신장(x2) + x… = 체중(y)“ 이다.
가설 정의
현실 세계에서 납득할 수 있는 가설은 총 3개를 구할 수 있다.
-허리 둘레가 크면 몸무게가 높다.
-가슴 둘레가 크면 몸무게가 높다.
-신장이 크면 몸무게가 높다.
즉, 최종 가설은 “허리 둘레, 가슴 둘레, 신장이 크면 그만큼 몸무게 또한 크다.” 이다.
[학습 알고리즘] – 개요
보통 위의 가설과 같이 선형의 구조를 갖고 있는 경우, 학습 알고리즘은 선형 회귀를 선택한다. 선형 회귀는 선형 예측 함수를 사용해 회귀식을 모델링하며, 알려지지 않은 파라미터는 데이터로부터 예측한다. 즉, 데이터[허리 둘레(x1), 가슴 둘레(x2), 신장(x3)]로 부터 알려지지 않은 파라미터[체중(y)]를 예측한다.
학습 방법 - [학습 알고리즘] – 설명
선형회귀 알고리즘을 시각화하면 다음과 같다.
-선형 회귀는 일차방정식 처럼 W와 b에 의해 가설 H 값이 달라진다.
-만약 허리 둘레, 가슴 둘레, 신장과 같이 값이 2개 이상일때는 선형 회귀(2)와 같다.
-우리는 H(X) = XW를 통해 다중 선형 회귀 또한 구성할 수 있다.

비용 함수
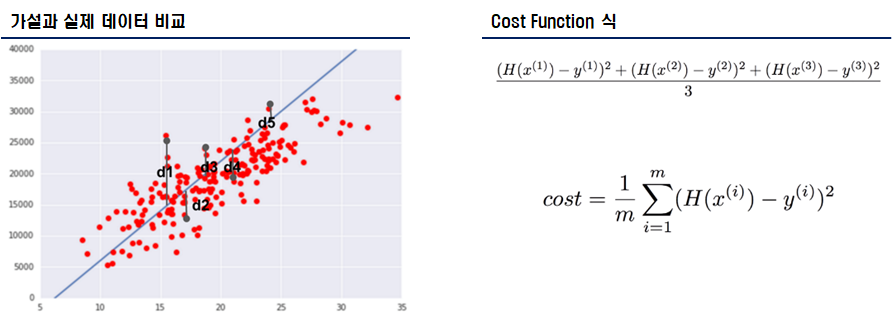
선형 회귀 알고리즘의 학습 정확도를 올리기 위해서는 cost 또는 loss를 줄여야한다. 가설과 실제 데이터 점의 거리가 짧아야 좋은 것이다. 즉, 더 좋은 가설을 판단하기 위해서는 가설의 점과 실제 데이터의 점을 비교한다. 해당 점이 짧은 것이 좋은 가설이며, 해당 거리를 측정해주는 것을 cost/loss function이라 칭한다.
선형 회귀의 Cost Function 식은 보통 (H(x)-y)^2 이다. 만약 2개 이상의 값이 있을 경우, Cost Function 식 그림과 같이 시그마 합 공식으로 표현할 수 있다. 해당 값을 작게 구하는 것이 선형 회귀의 학습이다.
옵티마이저
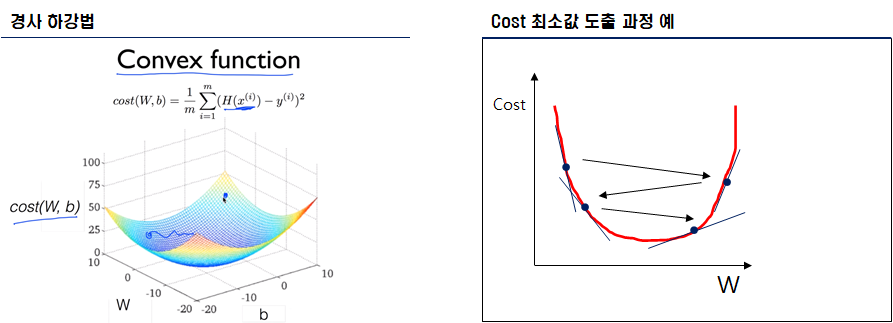
- Cost Function의 최소값을 찾는 알고리즘을 옵티마이져라 한다. 해당 프로젝트는 경사 하강법(Gradient Descent) 옵티마이져를 통해 최소값을 구한다.
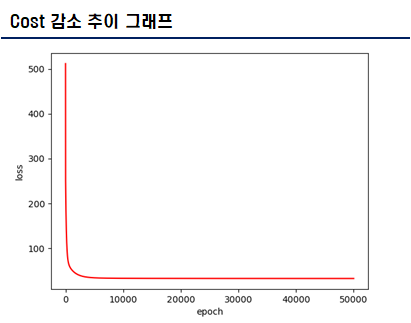
- 지속적인 반복 학습을 통해 Cost의 최소 값을 도출한다.
- 그러나, 데이터의 선형성이 존재하지 않으면 제대로된 Cost 감소를 실현하지 못한다.
학습
- 해당 가설을 입증하기 위해 선형 회귀(Linear Regression)알고리즘을 통해 학습을 진행
- Cost를 최소화 하기 위해, 경사하강법(Gradient Descent) 알고리즘을 적용
- 경사하강법의 학습 폭은 학습률(Learning Rate)을 통해 조절
- 학습률(Learning Rate)은 0.000015이다.
- 135,670개의 데이터를 5만번 학습 시켰으며, 학습률은 0.000015이다. 최종 Cost는 약 32.7382이다. 준수한 Cost를 얻었다.
데이터 검증
제일 중요한 부분이다. 우리가 가설을 정의하고 알고리즘을 선정하고 학습 시킨 모델이 제대로된 결과를 예측하는지 확인해야한다.
- 제일 좋은 방법은 데이터셋이 많을 경우, 데이터셋 중 1%만 검증에 사용하는 것이다.
- 또한 현실 세계에서 계측할 수 있으면 해당 값을 검증 데이터로 활용할 수 있다.
- 학습된 모델을 로컬 디스크에 저장하여, 해당 모델을 이용하여, 검증을 실시한다.
|
항목 |
순번 |
신장 |
허리둘레 |
가슴둘레 |
머리둘레 |
발 길이 |
실몸무게 |
예상치 (AI 계산) |
오차(kg) |
비고 |
|
검증 데이터 |
1 |
170.0 |
72.6 |
83.4 |
60.8 |
27.1 |
50.2 |
52.099712 |
+2 |
|
|
2 |
173.0 |
75.6 |
84.8 |
59.6 |
29.3 |
57.4 |
56.72512 |
-1 |
||
|
3 |
177.8 |
76.0 |
94.6 |
59.6 |
29.5 |
65.7 |
64.838196 |
-1 |
||
|
4 |
181.1 |
82.1 |
91.1 |
59.1 |
29.2 |
67.8 |
66.06932 |
-1 |
||
|
5 |
175.3 |
90.3 |
97.3 |
61.0 |
29.6 |
76.5 |
72.91974 |
-4 |
오차 벗어남 |
|
|
6 |
173.7 |
89.0 |
97.1 |
58.9 |
26.5 |
81.3 |
73.65506 |
-8 |
오차 벗어남 |
|
|
7 |
172.4 |
101.3 |
101.7 |
59.1 |
27.8 |
82.4 |
83.767784 |
+1 |
||
|
8 |
186.9 |
97.9 |
97.6 |
60.8 |
29.9 |
86.7 |
78.1594 |
-8 |
오차 벗어남 |
|
|
9 |
170.0 |
98.4 |
106.5 |
61.3 |
29.0 |
86.8 |
83.62165 |
-3 |
||
|
10 |
175.2 |
92.8 |
108.1 |
60.2 |
30.9 |
88.0 |
83.75437 |
-5 |
오차 벗어남 |
|
|
11 |
179.0 |
103.8 |
106.9 |
59.5 |
28.3 |
91 |
89.168076 |
-2 |
||
|
12 |
175.4 |
111.7 |
118.0 |
60.6 |
28.2 |
101.1 |
100.55304 |
-1 |
||
|
실세계 검증 데이터 |
13 |
183.2 |
98 |
102 |
61 |
28 |
87.5 |
80.801865 |
-7 |
오차 벗어남 |
|
14 |
181 |
115 |
121 |
60.5 |
28 |
107 |
105.02866 |
-2 |
||
|
15 |
173 |
85 |
89.5 |
56 |
26.5 |
68 |
68.778595 |
- |
||
|
16 |
176 |
92 |
107 |
61 |
28 |
82 |
81.05168 |
-1 |
||
|
17 |
172 |
108 |
110 |
59 |
28 |
96 |
93.85968 |
-3 |
||
|
18 |
174.1 |
98 |
105 |
58 |
26.8 |
83 |
85.66101 |
-2 |
요약
- 사용자의 신장, 허리 둘레, 머리 둘레, 가슴 둘레, 발 길이를 통해 체중 예측
- 가설을 입증하기 위해 선형 회귀(Linear Regression)알고리즘을 통해 학습을 진행
- Cost를 최소화 하기 위해, 경사하강법(Gradient Descent) 알고리즘을 적용
- 경사하강법의 학습 폭은 학습률(Learning Rate)을 통해 조절
- 학습률(Learning Rate)은 0.000015이다.
- 135,670개의 데이터를 5만번 학습 시켰으며, 학습률은 0.000015이다. 최종 Cost는 약 32.7382이다. 준수한 Cost를 얻었다
- 데이터의 매칭률은 72.22%이다.
한계
- 체질량 지수(Body Mass Index, BMI)의 문제점은 순전히 키와 몸무게를 통해 비만을 판정한다.
- 해당 사항의 문제점은 체지방 비율, 근육량, 뼈밀도 등의 데이터가 배제되었다는 것이다.
- 현재 데이터 또한 해당 사항을 배제하였다.
- 결국 오차는 근육량, 체지방 비율, 뼈밀도 등의 값이 평균치 보다 많거나 적을 때 생길 수 있다.
- 즉, 추가적으로 필요한 데이터셋은 나이, 근육량, 체지방량, 뼈밀도 이다. 해당 데이터셋을 통해 Cost를 5이하 최소화할 수 있을 것이다.
GitHub
https://github.com/ehdvudee/learn-tensor-project
ehdvudee/learn-tensor-project
Contribute to ehdvudee/learn-tensor-project development by creating an account on GitHub.
github.com
'개발관련 > 삽질' 카테고리의 다른 글
| Java Enum 활용기(기본/활용/Spring/MyBatis/테스트까지) (2) | 2020.07.20 |
|---|---|
| 샤미르의 비밀 공유(SSS, Shamir's Secret Sharing) - 구현 (0) | 2020.05.12 |
| 샤미르의 비밀 공유(SSS, Shamir's Secret Sharing) - 이론 (6) | 2020.05.07 |
| REST API 속도 개선(Java/Spring/Cache) (0) | 2020.02.27 |
| SQLite 개념/구조/멀티 DB 실사용기 (0) | 2020.01.08 |
