샤미르의 비밀 공유(SSS, Shamir's Secret Sharing) - 구현
목차
개요
클래스 및 메소드 소개(중요사항만)
코드 분석(중요사항만)
개요
SSS의 구현체를 분석한다. 분석 대상은 오픈 소스이다. 분석 대상 프로젝트의 링크는 다음과 같다.
https://github.com/timtiemens/secretshare
프로젝트 선정 기준은 다음과 같다.
-
개발 언어 유형 – Java
-
높은 스타 지수
-
샘플 파일 및 최소한의 문서(READEME.md)
클래스 및 메소드 소개(중요사항만)
[SecretShare.class(중요사항만 기재)]
| 내부 클래스 | 메소드 | 설명 | 비고 |
| PublicInfo | - |
Secret Share를 생성하기 위한 공개 정보를 보관한다. 공개 정보는 아래와 같다. - k: (t, n) 구성 요소 중 t에 해당하는 값이다. 비밀을 만들기 위한 비밀 조각들의 임계치 값(최소 개수 값) - n: (t, n) 구성 요소 중 n에 해당하는 값이다. 생성하고자 하는 비밀 조각들의 개수이다. - primeModulus: 비밀을 만들 때 사용하는 소수 값이다. - Description Info: 기타 정보 모든 메소들은 유틸성이다. |
|
| SplitSecretOutput | - | split 메스도를 통해 반환되는 객체이다. 사용자는 해당 객체를 이용해서 시크릿 조각들을 사용할 수 있다. | |
| ShareInfo | - | 시크릿 조각을 갖고 있는 객체이다(x, y 값). | |
| CombineOutput | - | 시크릿 조각 조합 후의 객체 | |
| - | split | 시크릿 조각들을 생성한다. | |
| - | combine | 시크릿 조각 조합(비밀 생성) |
[유틸 클래스(중요사항만 기재)]
| 내부 클래스 | 메소드 | 설명 | 비고 |
| PolyEquationImpl |
- |
다항 방정식을 처리하는 유틸클래스이다. |
|
| calculateFofX |
x 값을 정의하면, 해당 값으로 방정식의 계산을 실시한다. 예는 다음과 같다. fx = 1234 + 166x + 94x2 위의 값에 x가 1일 경우, 1494를 반환한다. |
||
| NumberSimplex | - |
선형대수 관련 연산을 할 때 사용. 시크릿 조각을 조립할 때 사용하는 핵심 클래스 |
|
| BigRational | - | 큰 값의 유리수 처리 | |
| Numbermatrix | - | Number를 확장한 객체에 대해 행렬을 형성해주는 클래스 |
코드 분석(중요사항만)
[분석 대상]
- SecretShare.split 메소드
- SecretShare.combine 메소드
[SecretShare.split]
개요
예: PublicInfo객체의 맴버 변수를 다음과 같이 지정한다.
- n = 16
- k = 3
- prime = 1613
위를 해석하면 16개의 조각을 생성하며, 3개의 조각은 임계치를 뜻한다. 즉, 3개의 조각이 존재할 경우 Secret을 생성할 수 있다. k가 3을 뜻하는 것은 이차방정식 그래프를 생성한 다는것이다. 예를 들면 아래와 같다(1234는 시크릿이다.).
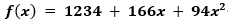
코드 분석
if (secret == null)
{
throw new SecretShareException("Secret cannot be null");
}
if (secret.signum() <= 0)
{
throw new SecretShareException("Secret cannot be negative");
}
if (publicInfo.getPrimeModulus() != null)
{
checkThatModulusIsAppropriate(publicInfo.getPrimeModulus(), secret);
}
- 유효성 검사를 실시한다.
BigInteger[] coeffs = new BigInteger[publicInfo.getK()];- k를 조회하여, k개의 계수를 생성한다 coeffs는 coefficient(계수)의 줄임말을 의미한다.
- 계수 1개의 수준은 1개의 Array이다.
randomizeCoeffs(coeffs, random, publicInfo.getPrimeModulus(), secret);
private void randomizeCoeffs(final BigInteger[] coeffs, final Random random, final BigInteger modulus, final BigInteger secret)
{
for (int i = 1, n = coeffs.length; i < n; i++)
{
BigInteger big = null;
//big = coeffGenOriginal(random); // see Issue#8
big = coeffGenImproved(random, modulus);
// FIX? TODO:? FIX?
big = big.abs(); // make it positive
coeffs[i] = big;
// Book says "all coefficients are smaller than the modulus"
if (modulus != null)
{
coeffs[i] = coeffs[i].mod(modulus);
}
// FIX? TODO: FIX? experiment says "all coefficients are smaller than the secret"
coeffs[i] = coeffs[i].mod(secret);
}
}
- Secret보다 작고, Prime보다 작은 Secret을 제외한 계수들을 생성한다.
- 예를들면 S가 1234이고 k가 3일 때 S를 제외한 1차항, 2차항에 대해 랜덤 계수를 생성한다.
- 0차항의 자리는 S 1234 값이 들어간다.
coeffs[0] = secret;- 0차 항은 S 값이다.
SplitSecretOutput ret = new SplitSecretOutput(this.publicInfo, equation);
for (int x = 1, n = publicInfo.getNforSplit() + 1; x < n; x++)
{
final BigInteger fofx = equation.calculateFofX(BigInteger.valueOf(x));
BigInteger data = fofx;
if (publicInfo.primeModulus != null)
{
data = data.mod(publicInfo.primeModulus);
}
final ShareInfo share = new ShareInfo(x, data, this.publicInfo);
if (publicInfo.primeModulus != null)
{
if (data.compareTo(publicInfo.getPrimeModulus()) > 0)
{
throw new RuntimeException("" + data + "\n" + publicInfo.getPrimeModulus() + "\n");
}
}
ret.sharesInfo.add(share);
}
return ret;
- x값은 1부터 시작하기 때문에 1부터 시작하여, n값(16) 까지 반복을 실시한다.
- calculateFofX를 통해 방정식의 셈을 실시한다.
- 해당 결과 값에 대해 mod를 실시한다.
- 생성한 Secret 조각들은 ShareInfo 객체에 적재한다.
- ShareInfo 객체는 SplitSecretOutput에 적재, 사용자는 최종적으로 SplitSecretOutput을 반환 받는다.
- 해당 과정은 다음의 그림을 만드는 과정과 같다.

[SecretShare.combine]
개요
ShareInfo는 다음과 같다.
- (1, 1494)
- (2, 329)
- (3, 965)
위의 ShareInfo 객체는 비밀을 만들기 위해 사용되는 비밀 조각들이다. 해당 조각들을 이용하여 combine 메소드를 실행한다. 해당 메소드는 불필요한 부분이 많기 때문에 해당 부분은 전부 설명에서 제외하였다.
코드 분석
CombineOutput ret = null;
sanityCheckPublicInfos(publicInfo, usetheseshares);
if (true)
{
println(" SOLVING USING THESE SHARES, mod=" + publicInfo.getPrimeModulus());
for (ShareInfo si : usetheseshares)
{
println(" " + si.share);
}
println("end SOLVING USING THESE SHARES");
}
if (publicInfo.getK() > usetheseshares.size())
{
throw new SecretShareException("Must have " + publicInfo.getK() +
" shares to solve. Only provided " +
usetheseshares.size());
}
checkForDuplicatesOrThrow(usetheseshares);
예외 처리
BigInteger[][] matrix = ele.getMatrix();
NumberMatrix.print("SS.java", matrix, out);
println("CVT matrix.height=" + matrix.length + " width=" + matrix[0].length);
BigRationalMatrix brm = BigRationalMatrix.create(matrix);
NumberMatrix.print("SS.java brm", brm.getArray(), out);
NumberSimplex<BigRational> simplex = new NumberSimplex<BigRational>(brm, 0);
simplex.initForSolve(out);
simplex.solve(out);
BigRational answer = simplex.getAnswer(1);
if (publicInfo.getPrimeModulus() != null)
{
solveSecret = answer.computeBigIntegerMod(publicInfo.getPrimeModulus());
}
else
{
solveSecret = answer.bigIntegerValue();
}
- 제일 중요한 부분이다.
- 역행렬 연산을 통해 선형 방정식을 계산한다.
- simplex.initForSolve(out);
-> 해당 메소드에서 역행렬을 진행하기 위한 행렬을 생성한다.
- simplex.solve(out);
-> 역행렬 작업을 진행한다.
-> 역행렬 작업은 NumberSimplex.createAbar(E[][] array, int I, int j) 메소드에서 진행한다.
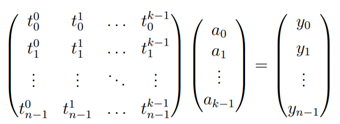
- 위와 같은 선형 방정식 행렬을 역행렬 작업을 진행한다.

- 위와 같이 3x3 행렬이 있다.

- 역행렬 공식은 위와 같다. 위의 작업을 simplex.solve(out)에서 진행한다.

- 역행렬 작업이 끝나면 위와 같이 행렬이 구성되어 있다.
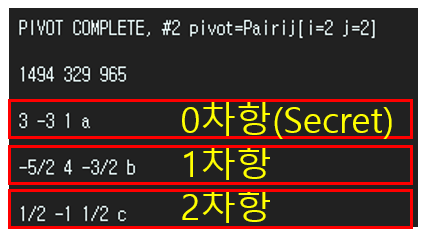

- 위의 행렬을 토대로 NumberSimplex.solve 메소드에서 computeAnswers 메소드를 통해 행렬 곱을 진행한다.
BigRational answer = simplex.getAnswer(0);
if (publicInfo.getPrimeModulus() != null)
{
solveSecret = answer.computeBigIntegerMod(publicInfo.getPrimeModulus());
}
else
{
solveSecret = answer.bigIntegerValue();
}
- simplex.getAnswer(0) // 리턴 씨크릿
- modulo 1613 작업을 진행한다.
'개발관련 > 삽질' 카테고리의 다른 글
| LoRaWAN 1.1 보안 부분 분석(LoRa Spec 6장 일부분 번역) (0) | 2021.02.04 |
|---|---|
| Java Enum 활용기(기본/활용/Spring/MyBatis/테스트까지) (2) | 2020.07.20 |
| Python TensorFlow를 이용한 몸무게 예측 프로그램 (0) | 2020.05.07 |
| 샤미르의 비밀 공유(SSS, Shamir's Secret Sharing) - 이론 (6) | 2020.05.07 |
| REST API 속도 개선(Java/Spring/Cache) (0) | 2020.02.27 |
